Pythagorean Theorem / Dalil Pythagoras
THE HISTORY OF PYTHAGORAS
Pythagoras adalah seorang matematikawan yang lahir sekitar tahun 582 SM. di Pulau Samos, Yunani. Pythagoras hidup amat sederhana, keras, dan memakai waktunya mengerjakan matematika. Pythagoras yakin bahwa matematika menyimpan semua rahasia alam semesta dan dia percaya bahwa beberapa angka memiliki keajaban. Pythagoras diingat karena dalil Pythagoras, sebuah rumus sederhana dalam geometri tentang ketiga sisi dalam segitiga siku - siku. Namun, Pythagoras juga melakukan beberapa eksperimen ilmiah paling pertama melalui mendengarkan suara senar yang diregangkan dengan panjang yang berbeda dan meneliti matematika oktaf dan harmoni. Ide - ide matematika Pythagoras menjadi penting bagi filsuf Plato dan melalui pengaruh Plato para ilmuwan lain seperti Galileo, Kepler, dan Sir Issac Newton.
Pada tahun 2500 SM, orang-orang Mesir Kuno menganggap pasangan bilangan 3,4 dan 5 sebagai bilangan-bilangan yang ajaib dan menyebutnya sebagai salah satu ajaran dari Dewa Oasis. Ketika mereka membangun fondasi piramida, mereka menggunakan bilangan-bilangan tersebut sebagai acuan membangun sudut siku-siku dengan bantuan sebuah tali yang dibuat 4 simpul dengan jarak masing-masing antara simpul pertama dan kedua berjarak 3 satuan, simpul kedua dan ketiga berjarak 4 satuan dan simpul ketiga dan keempat berjarak 5 satuan. Jika tali tersebut dibuat segitiga dengan menyatukan simpul pertama dan keempat, maka didapatkan sbeuah segitiga siku-siku yaitu suatu segitiga yang salah satunya siku-siku.
DALIL PYTHAGORAS
Kita nyatakan sisi BC (sisi di depan sudut A) dengan a,sisi AC (sisi di depan sudut B) dengan b, sisi AB (sisi di depan sudut C) dengan C Berdasar dalil Pythagoras berlaku : c2 = a2 + b2 atau AB2 = BC2 + AC2, atau b2 = c2 – a2 atau a2 = c2 – b2
Kesimpulan yang diperoleh dari dalil Pythagoras untuk sisi-sisi segitiga yaitu :
Dalam segitiga ABC siku-siku dengan sisi-sisi a, b, dan c berlaku :
1. Bila segitiga ABC siku-siku di A berlaku a2 = b2 + c2
2. Bila segitiga ABC siku-siku di B berlaku b2 = a2 + c2
3. Bila segitiga ABC siku-siku di C berlaku c2= a2 + b2
Berlatih dulu yuuk …
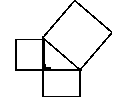
1.Perhatikan gambar berikut :
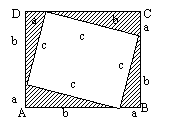
a. Berapakah luas persegi diatas?
b. Hitung luas daerah yang diarsir !
c. Berapa luas daerah yang tidak diarsir ?
d. Kesimpulan apa yang bisa didapat ?
2. Diketahui sisi-sisi beberapa segitiga, tentukan apakah segitiga siku-siku, lancip, atau tumpul ? Kemukakan alasannya !
Segitiga ABC dengan a = 5 cm, b = 6 cm, dan c = 8 cm
Segitiga PQR dengan p = q = r =6 cm
Segitiga ABC dengan a = 9 cm dan b = c = 12 cm
Segitiga KLM dengan m = 10 cm, k = 16 cm dan l = 18 cm
3. Diketahui segitiga PQR siku-siku di Q. Panjang hipotenusa segitiga PQR adalah 8 , dan sudut P = 300
Tentukan panjang PQ dan QR dan tentukan luas daerah segitiga PQR
4. Sebuah segitiga ABC siku-siku di B dan Besar sudut BAC = 300. Jika luas segitiga itu adalah 8 cm2, hitunglah panjang sisi-sisi segitiga tersebut !
Pythagoras adalah seorang matematikawan yang lahir sekitar tahun 582 SM. di Pulau Samos, Yunani. Pythagoras hidup amat sederhana, keras, dan memakai waktunya mengerjakan matematika. Pythagoras yakin bahwa matematika menyimpan semua rahasia alam semesta dan dia percaya bahwa beberapa angka memiliki keajaban. Pythagoras diingat karena dalil Pythagoras, sebuah rumus sederhana dalam geometri tentang ketiga sisi dalam segitiga siku - siku. Namun, Pythagoras juga melakukan beberapa eksperimen ilmiah paling pertama melalui mendengarkan suara senar yang diregangkan dengan panjang yang berbeda dan meneliti matematika oktaf dan harmoni. Ide - ide matematika Pythagoras menjadi penting bagi filsuf Plato dan melalui pengaruh Plato para ilmuwan lain seperti Galileo, Kepler, dan Sir Issac Newton.
Pada tahun 2500 SM, orang-orang Mesir Kuno menganggap pasangan bilangan 3,4 dan 5 sebagai bilangan-bilangan yang ajaib dan menyebutnya sebagai salah satu ajaran dari Dewa Oasis. Ketika mereka membangun fondasi piramida, mereka menggunakan bilangan-bilangan tersebut sebagai acuan membangun sudut siku-siku dengan bantuan sebuah tali yang dibuat 4 simpul dengan jarak masing-masing antara simpul pertama dan kedua berjarak 3 satuan, simpul kedua dan ketiga berjarak 4 satuan dan simpul ketiga dan keempat berjarak 5 satuan. Jika tali tersebut dibuat segitiga dengan menyatukan simpul pertama dan keempat, maka didapatkan sbeuah segitiga siku-siku yaitu suatu segitiga yang salah satunya siku-siku.
DALIL PYTHAGORAS

Kita nyatakan sisi BC (sisi di depan sudut A) dengan a,sisi AC (sisi di depan sudut B) dengan b, sisi AB (sisi di depan sudut C) dengan C Berdasar dalil Pythagoras berlaku : c2 = a2 + b2 atau AB2 = BC2 + AC2, atau b2 = c2 – a2 atau a2 = c2 – b2
Kesimpulan yang diperoleh dari dalil Pythagoras untuk sisi-sisi segitiga yaitu :
Dalam segitiga ABC siku-siku dengan sisi-sisi a, b, dan c berlaku :
1. Bila segitiga ABC siku-siku di A berlaku a2 = b2 + c2
2. Bila segitiga ABC siku-siku di B berlaku b2 = a2 + c2
3. Bila segitiga ABC siku-siku di C berlaku c2= a2 + b2
Berlatih dulu yuuk …
1.Perhatikan gambar berikut :

a. Berapakah luas persegi diatas?
b. Hitung luas daerah yang diarsir !
c. Berapa luas daerah yang tidak diarsir ?
d. Kesimpulan apa yang bisa didapat ?
2. Diketahui sisi-sisi beberapa segitiga, tentukan apakah segitiga siku-siku, lancip, atau tumpul ? Kemukakan alasannya !
Segitiga ABC dengan a = 5 cm, b = 6 cm, dan c = 8 cm
Segitiga PQR dengan p = q = r =6 cm
Segitiga ABC dengan a = 9 cm dan b = c = 12 cm
Segitiga KLM dengan m = 10 cm, k = 16 cm dan l = 18 cm
3. Diketahui segitiga PQR siku-siku di Q. Panjang hipotenusa segitiga PQR adalah 8 , dan sudut P = 300
Tentukan panjang PQ dan QR dan tentukan luas daerah segitiga PQR
4. Sebuah segitiga ABC siku-siku di B dan Besar sudut BAC = 300. Jika luas segitiga itu adalah 8 cm2, hitunglah panjang sisi-sisi segitiga tersebut !
0 comments:
Post a Comment